You got nothing on the 17 square packing
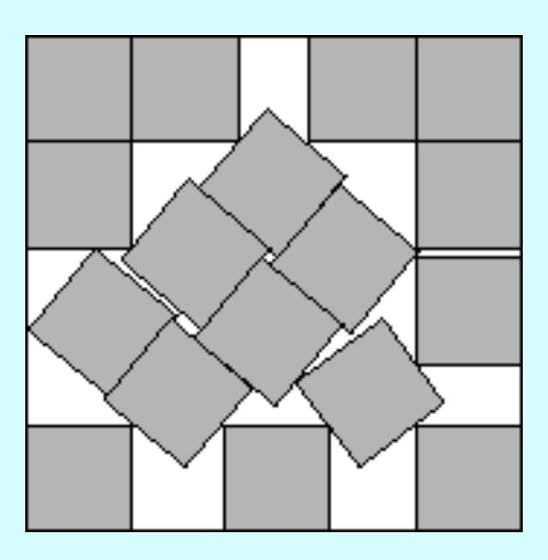
Can someone explain this?
This is the most efficient (known) packing of 17 unit squares inside a square. If you’re asking why it’s like that, that’s above my math proficiency level.
https://en.wikipedia.org/wiki/Square_packing
See also: https://kingbird.myphotos.cc/packing/squares_in_squares.html
Thanks I’ve lost 30 sanity points now, and I’m now sure with a number of squares sufficently high s is gonna equal to cthulu.
It’s like that because the universe wants us to suffer.
No, suffering would be if it were always the same predictable pattern in everything all the time.
True. You can’t have joy without suffering, light without dark, cars without an extended warranty.
If God was real / or is real and cared, we would have a perfect 336 day year.
If God was real the boxes would all fit in a nice grid for any square container. But the OP already has the conclusion for that one.
We’ve figured out optimal packing methods for any number of squares inside a big square. When a number is below and near a square number like 15, you just leave an empty box, but when it’s far from the next square number, you’ll be able to pack them more efficiently than just leaving empty squares around. Turns out this kind of stuff is hilariously hard to prove that it’s the most efficient method.
Mathematics actually hates humanity, and it likes to remind us of it, sometimes. That’s why.
?

This is about the most efficient way to pack that number of circles. By looking at the bottom row of the 49, you can see that it’s slightly less wide than 7 diameters, because it has 5 circles at the very bottom (taking up 5 diameters of width), but two are slightly raised, which also means they’re slightly inward.
How?
Yes, if you push the circles down a bit, it forms a 7 by 7 matrix. But if pushing the circles into a square matrix is not allowed: how?
Edit: I get it now. It is about (efficient) packing not about counting. I also get the 4th panel now…
7 by 7 matrix isn’t the optimal packing. The square shown is slightly smaller than 7 by 7.
Thanks. I thought it was about counting. It all makes a lot more sense now. (And it also doesn’t.)
Yeah it can fit almost 7 in a line in the last panel so theese definitely aren’t the same squares(or circles)
These are optimal packings of n circles in a square container of the smallest size that will contain them
So it is fitting the 49 in smallest square and not fitting as many circles as possible in given square? Okay that makes sense
Correct!
I mean it makes sense when you think about how the circles arrange in an infinte square and e.g. 4r square. There has to be some fuckery between the perfect packing and the small square packing. You can see a triangle of almost perfect packing in the middle of the 49 circle square, surrounded by fault lines in the structure and then some more good packing, and garbage in the bottom.
slightly related Steve Mould video
Or, they could do 6x8 with one obviously extra at the end. But this is a funny not a rational thing.
Yarr
Neat spacing leave much gap, patterned mess less space between.
Well-put. One perfect pattern at one scale, another perfect pattern at a different scale, and then there has to be a transition between them of optimal steps along the way. I like that.
Should have used hexagons
That’s what she said 😏
The bestagons.
HCP FTW.
This is the kind of stuff the timber mafia needs to know so that they can efficiently pack trees and send them to IKEA.

deleted by creator
Because it’s a smaller area than 7x7.
If you consider the regular packing in an infinite plane, tri/hex packing is the most space efficient (least wasted space), so I’d assume larger packings would tend towards that. But in smaller packings, the efficiency loss from the extra size needed to offset the circles outweighs the efficiency gained by hex packing.
7x7 is the boundary where those efficiency tradeoffs switch.
Thank you for this explanation!
Trying to think how tri/hex is more efficient than any regular tiling, say squares.
Want a hint? Think about a circle bound by an n-sided polygon. What happens to the space between the bounding polygon and the circle as n increases? And when n is infinite?
So of three possible regular tilings, which will be most and least efficient?
(Btw, strictly speaking, I shouldn’t have said tri/hex before, as it’s really just hex tiling.)
You could also use some fancy trig to calculate the efficiency %, but that’s way too much work for me. :)
deleted by creator
I think you skipped a row.
Also, 6*6+7=???
I did yeah; deleted my content almost immediately after posting it because I went to double check. Counting is hard!
Maths is a science now?
Science is applied math, engineering is applied science, manufacturing is applied engineering, etc. it’s math all the way down.
Relevant XKCD: https://xkcd.com/435/

Math and philosophy are basically interchangeable here. I know there’s a maths version I saved somewhere. 😅
I mean without philosophy there is no math
And vice versa.
Wdym?
Math and formal logic are effectively equivalent and philosophy without conditional logic is useless. Scientifically useful philosophy is just “explorative logic” or something like it
Science and philosophy are two sides of the same coin: the basic building blocks of how we perceive the world around us. Both need each other. Logic is often taught in maths classes. It’s a bit like how to build a program (in this metaphor, it’s how our brains percieve and interact through the world), a little but of intent, and a little bit of code.
Without computation there’s neither which is why CS always wins.
always_has_been.jpg
We’ve got !mathmemes@lemmy.blahaj.zone for maths but it’s a bit quiet compared to here
Quality over quantity! 😉

I think you forgot the /s
The study and discovery of mathematics is, yes.
Always has been.














